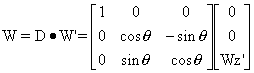
Therefore:          return

(9)

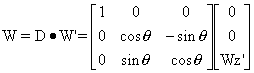
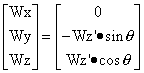
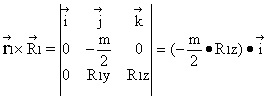
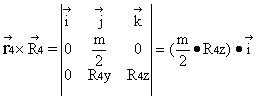
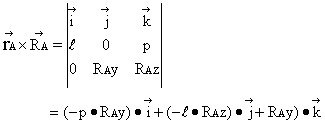
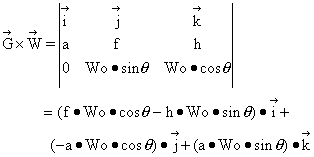
From Eq.(4): (4)'

From Eq.(5): (5)'

From Eq.(6): (6)'

From Eq.(5)': (10)

From Eq.(6)': (11)

Substituting Eg.(10) into (3):

(12)

Substituting Eq.(11) into (4)':

(13)

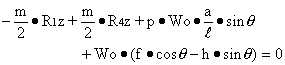
With Eq.(12):

(12)'

With Eq.(13):

(13)'

From [Eq.(12)' - Eq.(13)'x (2/m)]:

Therefore:

(14)

From [Eq.(12)' - Eq.(13)' x (2/m)]:

Therefore:

(15)

In Eq.(14), if we let:

and in Eq.(15), if we let:

we can have:

(16)

(17)

Similarly, if we substitute Eg.(11) into Eg.(2):

(18)

From Eqs.(16) and (17):

Therefore:

(19) (20)

Substituting Eq.(18) into Eq.(19):

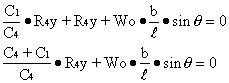
Therefore:

where:

such that:

And:

(21)

Substituting Eq.(18) into Eq.(20):

Therefore:

And:

Therefore:

(22)

With regards to the reaction forces R2 and R3 at the front wheel,

(23) (24)

(25)

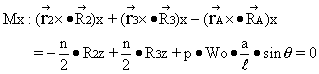
Also,

(26)

From [Eq.(24)-Eq.(25) x (2/n)]:

Therefore:

(27)

From [Eq.(24) + Eq.(25) x (2/n)]:

(28)

Where if:

then:

(29)

(30)

From Eqs.(26), (29) and (30):

(31)

and then,

Substituting Eq.(31) into (32):

Therefore:

(32)

Similarly,

(33)

Sample problem:

Perform the analysis for a three-wheeled tractor.

Solution:

From Eq.(10):

From Eq.(11):

With p = 0:

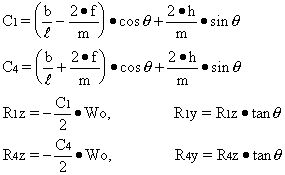
Sample problem:

Describe the condition when the center of gravity of the tractor is along the center line.

Solution:

If the center of gravity is at the center, f = 0, therefore:

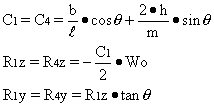
Sample problem:

Describe the condition when

Solution:

The tractor wheels are about to slide sideways.

Sample problem:

Describe the conditions for a lateral turn to occur about the line AB.

Solution:

R4z = 0, that is: C4 = 0

The lateral turn will occur when:

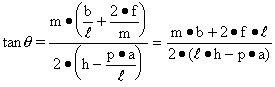
Sample problem:

In Figure 2-2, a = 50 cm, l = 160 cm, f = 20 cm, m =100 cm, and W = 1000 kg, derive the values of R1, R2 and R3.

Solution:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

From Eq.(6):

From Eg.(5):

(8)

Dividing Eq.(7) by 50:

(9)

Adding Eqs.(8) and (9),

Substracting Eq.(9) from Eq.(8),

     return