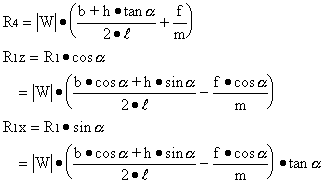By substitution into equations (1) to (6),          return 

(1)'

(3)'

(4)'

(5)'

　　(6)'

(7)'

From equation (7)'

Substituting into Eq. (1)',

(8)

From equation (3)'

(9)

Dividing equation (8) by equation (9),

K = tan a    (10)

(11)

(12)

(13)

From equation (5)', a direct derivation can be performed to give,

(14)

Therefore:

(15)

Substituting Eq.(14) into Eq.(3)',

(16)

From (16) + (4)'(2/m)

Therefore:

(17)

And:

(18)

Similarly, From (16) - (4)'(2/m)

Therefore:

(19)

And:

(20)

With regards to the front wheel:

(21)

(22)

Also,

(23)

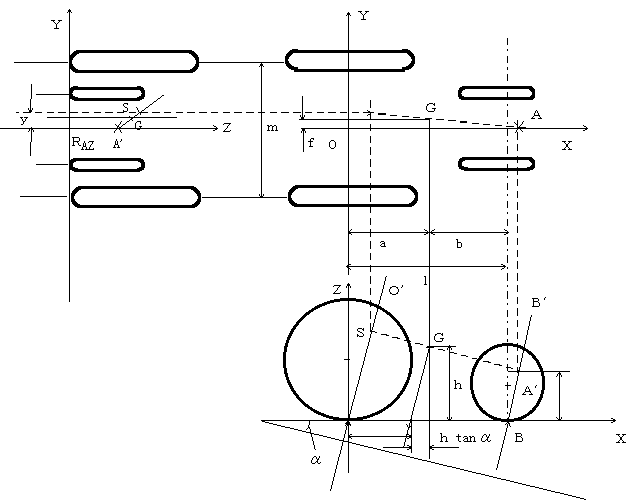
Figure 2-6. Geometry of the front-rear inclination

In order to explain (21)- (23) using geometry and ratio and proportion, we can take moments about 0 in Fig. 2-6,

where:

Therefore:

Accordingly:

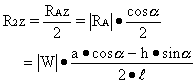
This equation compares well with Eq.(21).

Also:

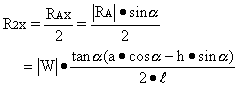
which compares well with Eq.(22).

If intersection point of the line joining A' and G and the plane on which R1 and R4 lie is represented as S(Sx,y, Sz),then:

Therefore:

With Rr as the reaction total force on the rear wheel,

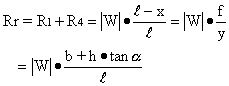
If we take moment about the contact point of the left rear wheel:

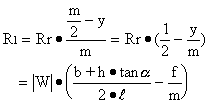
Similarly:

     return