2. Tractor static balance     return 

2-1. Tractor static balance (Two-dimensional system)

Generally, in the dynamics of balance, the following 2

equations hold:

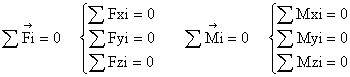
From here:

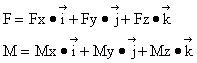
and:

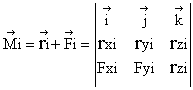
Therefore:

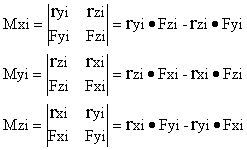
In Figure 2-1, when the tractor is stationary, and the thrust force F and resistance force P are both zero, the following equations hold true:

 

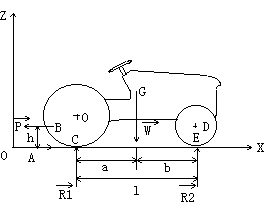
Figure 2-1 Tractor balance

(1)

 

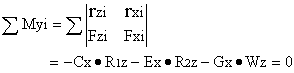(2)

 

where is the weight, is the center of gravity position vector and and are the position vectors of points C and E.

From (1) and (2):

 

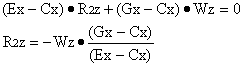(3)

Substituting (3) into (1) gives:

(4)

With directed downward, it is negative. Also, with:

and can be expressed by:

(5)

(6)

Sample problem:

A tractor has a weight of 800 kgf. Its center of gravity is 80cm from the rear wheel axis towards the front and 100 cm from the front wheel axis to the rear. Determine the reaction forces on both the front and rear wheels.

Solution:

Rear wheel: (kgf)

Front wheel: (kgf)

 

 

2-2. Static balance of a three-wheel tractor (3-dimensional)     return 

 

In going from two-dimensional to three-dimensional system of coordinates, it is necessary to consider another equation, equation (7) since the components of the forces like those of gravity and soil reaction, are not available for the X and Y axes.

(1)

(2)

(7)

Equation (7) gives:

 

(8)

 

Accordingly, in Figure 2-2, the balance of a stationary three-wheel tractor can be expressed by:

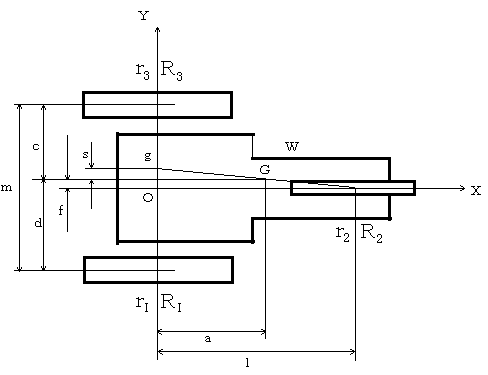
Figure 2-2 Three-wheeled tractor

 

(9)

(10)

(11)

 

From equations (9), (10) and (11), expressions for R1, R2 and R3 can be obtained. From [Eq.(9) x r_3y - Eq.(10)]:

(12)

 

From [Eq.(9) x r_3x + Eq.(11)]:

(13)

 

From [Eq.(12) x (r_3x-r_2x) - Eq.(13) x (r_3y - r_2y)]:

 

(14)

 

From [Eq.(12) x (r_3x - r_1x) - Eq.(13) x (r_3y - r_1y)]:

 

(15)

 

Substituting Eqs. (14) and (15) in Eq. (9):

 

(16)

 

Equations (14), (15) and (16) are the general expressions for the reactions on the three wheels.

Based on the positions, the following relationships can be established:

 

 

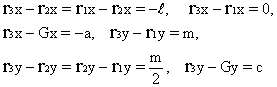
with which Eqs. (14), (15) and (16) become:

(17)

(18)

(19)

 

It can be clearly understood why the expression for R_2z is similar to that which was previously determined. With regards to R_1z and R_3z, if the center of gravity G is offset by a distance f Eqs. (17) and (19) can be modified such that:

 

(20)

 

(21)

Let g represent the point of intersection of the straight line r₂G and the axis of the rear wheels. In the previous discussion, the value of R₁z is given by:

 

 

With point g dividing the line segment r₁-r₂ = m, the equations for R_1z and R_3z can be derived.

It is because using the triangle or₂g,

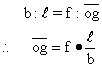
Working on the quantity inside the parenthesis of Eq.(20):

Also, for the quantity inside the parenthesis of Eq.(21):

 

Sample problem:

 

In Fig. 2.2, derive the reaction forces on both of the rear wheels when a) G is along the line or₂ and b) when G is along the line r₂r₃.

 

Solution:

a) When G is along or2,

C = d = m/2

and from Eqs.(20) and (21):

b) When G is along the line r₂r₃, from the ratio:

 

 

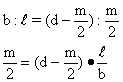
And using Eqs.(20) and (2)1:

 

     return