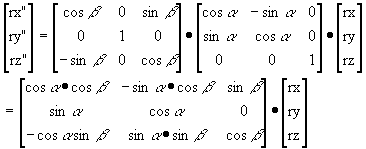1-7. Coordinate transformation    return to menu

A vector which is expressed in a particular system of coordinates may have its components expressed in terms of another system of coordinates.

Given the unit vectors , and and , and for the XYZ and X'Y'Z' coordinate systems,

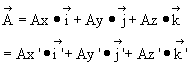
If the direction cosines of , and in the XYZ system are l1, m1, n1, l2, m2, n2, l3, m3 and n3:

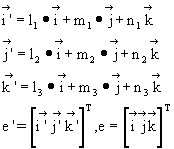
and if:

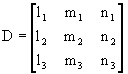
Also,

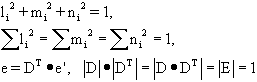
Based on the XYZ system, vector is given by:

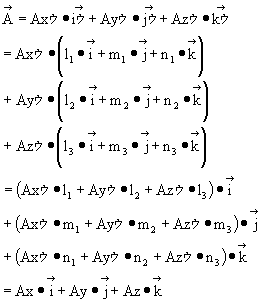
Therefore:

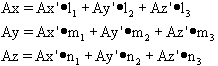
Consequently, if:

then:

Also:

Sample problem:

As shown in Figure 1-9, the X and Y axes rotate an angle 0 around the Z axis. Determine the new components of vector F in the X', Y' and Z' coordinate system .

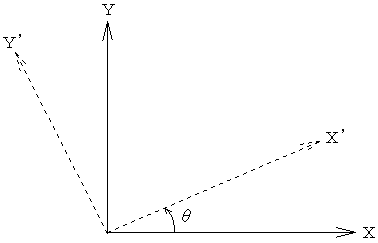
Figure 1-9

Solution:

The new unit vectors are:

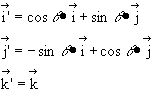
such that:

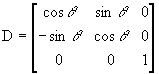
Accordingly: F' = D・F

or:

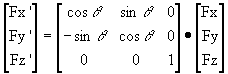
Sample problem:

In Figure 1-10, determine the components of vector r in the X", Y" and Z" coordinate system. This coordinate system is formed by, first,a) the rotation of the X and Y axes about Z axis by angle a, and then, b) by rotating the X' and Z' axes around Y' by angle B.

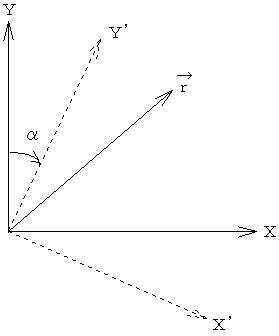
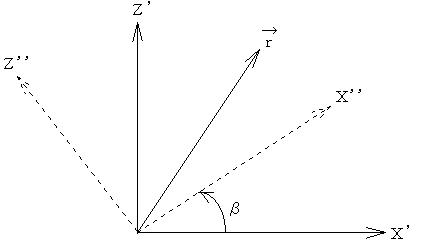
Figure 1-10(a) Figure 1-10(b)

Solution:

The unit vectors in the X' Y' Z' coordinate system are:

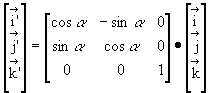
The unit vectors in the X" Y" Z" coordinate system are:

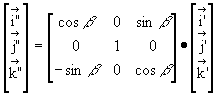
Therefore: