Sample problem:    return to menu

In Figure 1-8, the location position of point P is determined by the position vector . As point P traces the space curve, determine the tangent vector and the principal normal vector .

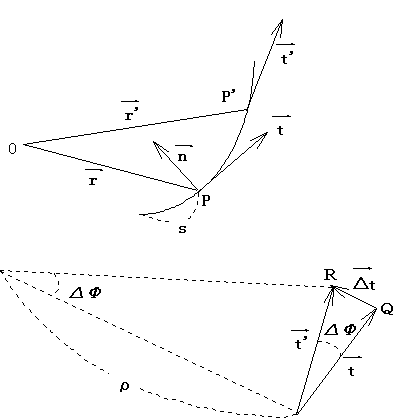
Figure 1-8 Space curve

Solution:

In Figure 1-8, when the length of the curve s is expressed using its parameters, = and PP' = △s, the tangent vector can be shown by:

The vector is tangent at point P, has a direction towards increasing s and has magnitude of 1 as a unit vector.

Using the components of along the X, Y and Z axes,

From points P and P' where vectors and are tangent respectively, can be obtained. In the triangle PQR, as △s approaches 0, |dt| approaches △φ. Therefore:

: the curvature

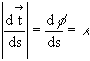
From the reciprocal of the curvature, the radius of curvature ρ can be obtained:

With and parallel, when △s approaches 0, become perpendicular to vector as is perpendicular to vector .

The unit vector which is normal to vector and lying on the osculating plane can be introduced as:

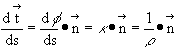
Therefore:

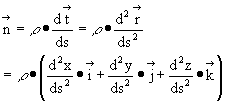
where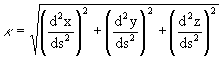

Another unit vector , which is perpendicular to both and can be introduced as:

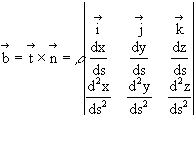
This vector is referred to as the binormal vector.

Sample problem:

Determine the velocity vector and the acceleration vector given the position vector of a point.

Solution:

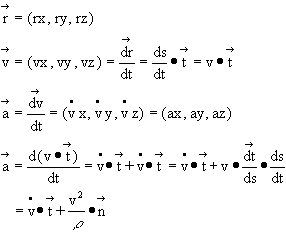
Therefore:

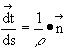
where = the unit tangent vector

ρ = the radius of curvature

　 = unit vector normal to

The acceleration vector can be determined using the tangential direction component and the principal normal direction component .

1-6. Integral of vectors

Given a vector function , its indefinite integral can be given by:

If , then

where is an arbitrary vector which has no relation to t.

Generally, the following relationships hold true: