1-4. Outer product return to menu
The vector whose magnitude is equal to the area of a parallelogram with two sides formed by vectors A and B and whose direction is perpendicular to the two vectors as determined following the right hand screw motion, is called the vector product (cross product) of vectors A and B and given by the following equation:
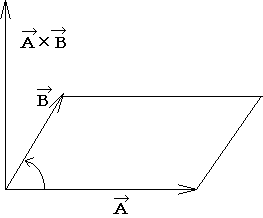
Figure 1-5. Vector cross product
The angle
θ is between vectors 
and 
and 
is a unit vector defining the direction of 
. The magnitude is given by
.
Cross
multiplication does not obey the commutative law such that the magnitudes of 
and 
are equal but their directions
are opposite, i. e.:
The
distributive law is however followed and
Using the X, Y
and Z coordinates, the product of two vectors and 
is given by:
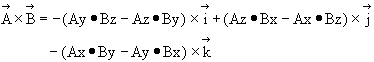
which were
based on the following relationships among the unit vectors:
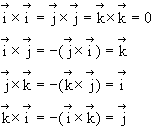
A simpler
computation can be performed using matrices.
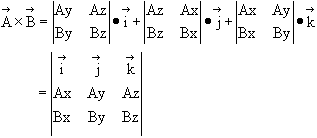
Sample problem:
Using Figure
1-6, describe vector 
whose direction is along the Z-axis and whose magnitude is
given by a F. Vector M is the cross product of vectors 
and 
which are on the XY plane.
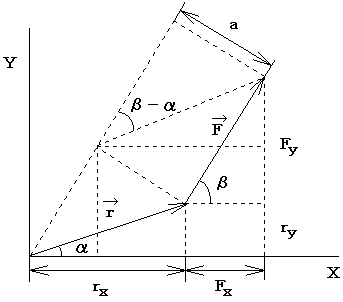
Figure 1-6 Geometry of cross multiplication of vectors
Solution:
If we let A as
the area of the parallelogram whose two sides are vectors and ,
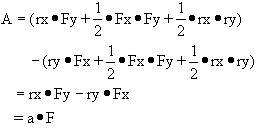
Therefore,
In another
method, the following can also be derived from the figure:
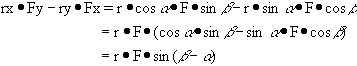
with 
,
Therefore,
1-5 Vector
differential
Let vector 
represents a variable
function of time t as shown in Figure 1-7. With a time increment of △t, vector also changes with an increment of △ from which the differential can be
determined.
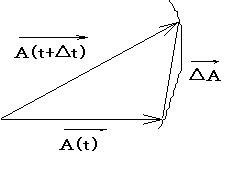
Figure 1-7 Vector differential
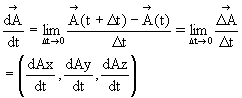
Also, the
differentials of the products when a vector is multiplied with a scalar
variable function λ and when it is multiplied with another vector are
given respectively:
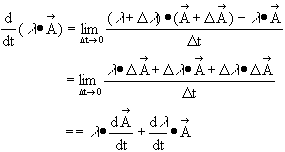
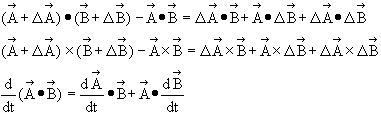
Therefore: 