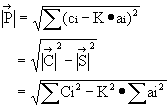Sample problem:     return to menu

Given a vector , determine its projection on another vector .

Solution:

If the projected component is called and , then:

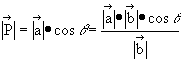
which becomes:

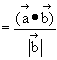
From the above, vector e is a unit vector along the direction of , such that:

Therefore:

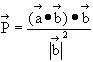
Showing the component parts, the vector is given by the equation:

Using the above equation for a three dimensional case, the equation becomes:

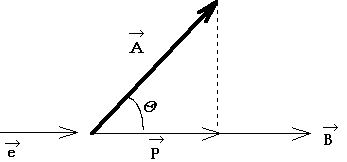
Figure 1-3. Projection of a vector on another vector

Sample problem:

Find the projection of vector C on the plane A provided that and the equation of the plane is given by:

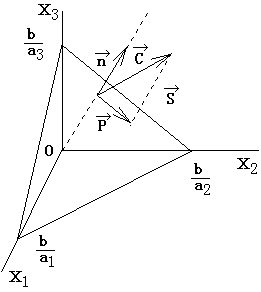
Figure 1-4. Projection of a vector on a plane

Solution:

A unit vector normal to plane A is given by

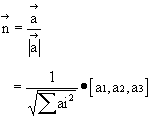
In, Fig. 1-4, if is the projection of on plane A, then

provided that is the projection of on .

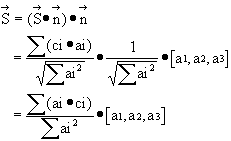
Therefore,

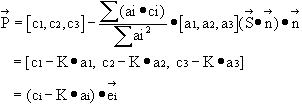
where:

and are unit vectors along the Cartesian coordinates. The magnitude of the is