1. Vector
1-1 Introduction return to menu
In performing analysis involving the dynamics of agricultural machinery, the use of vectors can present many clear and unified explanations.
The following advantages can be mentioned: 1) Explanatory diagrams can easily be illustrated; 2) Vectors have general application to both the two- and three- dimensional coordinate systems; 3) By computer programming, calculation procedures based on the given components can easily be performed.
1-2 Vectors return to menu
Vector quantities, as illustrated in Fig. 1.1, have both magnitude and direction in contrast with scalar quantities which have only magnitude.
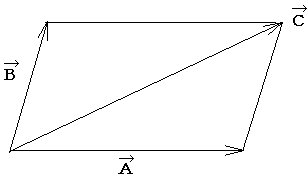
Figure 1-1. Sum of vectors
The
representation of a vector can be
,
or Ａ. In the above figure,was used.
Based on the
parallelogram law, resolution and decomposition of vectors in Fig. 1.1 can give
the following equation:
Based on the
XYZ coordinate system, the components of a vector can be expressed by the
following:
In this
equations, 
, 
and 
are the unit vectors along the x,
y and z rectangular coordinates, respectively. Ax, Ay and Az are the magnitudes
of components of along
the three directions.
The magnitude
of A can be expressed using the following equation:
1-3 Inner
product
The product of
multiplying the magnitudes of and 
and the value of the cosine of the angle between the two
vectors is called the scalar product (dot product). It is given by the
following formula:
As shown in
Figure 1-2, this is the product of the magnitude of and the magnitude of the component of on .
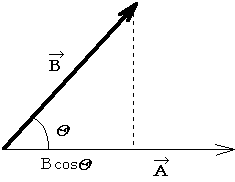
Figure 1-2. Scalar product
In general, the
commutative law and the distributive law are both followed such that:
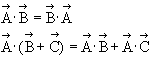
By using the
components of the vectors along the XYZ coordinates, the following
multiplication can be performed:
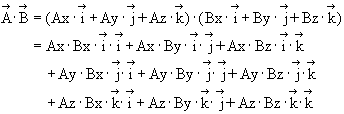
where the
products of the unit vectors are given by:
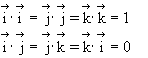
such that:
Sample problem:
Determine the
magnitude of the angle between two vectors and .
Solution:
Also:
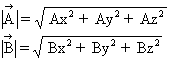
Therefore,
